[CS182] Lecture 18 - VAEs, invertible models
CS 182: Deep Learning
Head uGSI Brandon Trabucco btrabucco@berkeley.edu Office Hours: Th 10:00am-12:00pm Discussion(s): Fr 1:00pm-2:00pm
cs182sp21.github.io

이번 강의에선 latent variable model을 이어서 학습한 뒤 variational autoencoder, invertible model을 배운다.
우선 지난 강에서 배운 latent variable model에 대해 간단히 복습해보자.

Latent variable model은 p(x)의 distribution을 더 간단한 2개의 distribution으로 나누어 생각하는 것이다. p(z)와 p(x | z) 모두 쉬운 distribution이다. 다만 p(x | z)의 mean, variance는 z에 대한 deterministic complex neural network function이다. 따라서 위의 식처럼 p(x)는 p(z)와 learned model p(x | z)를 곱한 것의 integral로 이뤄진다.

그러나 integral 계산 시 가능한 모든 z에 대해 더할 수가 없어 not trackable하므로 대신 expected log-likelihood를 사용한다. z가 무엇인지 모르니, p(z | x_i)를 이용해 주어진 x_i에 대해 가장 그럴듯한 z를 찾아 joint probability를 최대화한다. 실제 사용 시에는 x의 일부를 샘플링해서 적용한다.
문제는 p(z | x_i)이다. 이를 probabilistic inference라고 하는데 어떤 z가 x_i에 가는지 "inferring"한다. 즉 어떤 latent variable이 특정한 image로 가는지를 확인하는 것인데, 지난 강의에선 이를 다루지 않았다. (있다고 하고 넘어갔다)

Inference는 굉장히 어렵다. 그래서 나온 아이디어가 실제 p(z | x_i)의 distribution을 계산하는 대신 더 다루기 쉬운 distribution을 이용해 approximate라는 것이다. 예를 들자면 각 i번째 image마다 각각 mean, variance가 있는데, 이 두 mean과 variance를 이용해 만든 새 distribution q_i를 사용해 p(z | x_i)를 estimate하는 것이다.

어떻게 하느냐 하면, 어떤 q_i에 대해서도 log probability 상에서 위 이미지에 따라 식을 변형할 시 lower bound가 있다는 것이 위의 Jensen's Inequality (concave function에 대한) 에 의해 알려져 있다. 그렇다면 그 lower bound를 증가시킬 수 있다면 자연스레 log probability도 증가할 것이다. 따라서 위 이미지 하단의 마지막 식의 term을 maximize한다면, log p(x_i)를 maximize하는 것과 비슷한 결과를 낳을 수 있다.

이를 더 자세히 알기 위해서는 정보이론에 대한 지식이 필요해 강의에서 잠깐 짚고 넘어간다.
먼저 entropy이다. 많이 들어본 단어인데, 여기서는 log probability의 expectation의 음수를 뜻한다. 이것이 뜻하는 바에 대한 몇 가지 설명이 있는데, 가장 와닿는 설명은 불확실성, 즉 "놀라움의 정도의 평균"를 뜻한다는 것이다. H(p)에서 p가 만약 uniform distribution이라면 모든 확률이 같아 불확실성이 최대이다. 이때 entropy도 최대가 된다. 반면, one-hot distribution처럼 어느 한 가지의 확률이 1이고 나머지가 0인 경우를 생각해보자. 반드시 특정한 것이 나오니 결과는 딱히 놀랍지도 않고, 불확실하지도 않다. 이때 entropy는 최저가 된다. 강의에서는 random variable이 얼마나 random한지라고도 했고, 이 역시 entropy를 이해하는 데 도움이 되었다(앞의 설명과 동일한 말이라고 생각한다. 하나가 정해져 있다면 random variable이 random하지 않은 것이니).
최대화해야 하는 식을 보면 expected log probability와 entropy term이 있는데, 둘 모두를 최대화햐아 한다. Expected log probability의 경우는 q_i가 p(x_i, z)가 가장 큰 점에 가장 큰 "mass"를 부여하도록 해서 최대화할 수 있다. 다만 entropy term 역시 최대화햐아 하고, 이를 위해선 q_i의 분포가 보다 넓어야 한다.

다음으로 필요한 것은 KL-Divergence이다. 간단히 말하자면, 두 분포가 얼마나 차이나는지에 관한 값이라고 생각하면 된다. 또는, 이 식을 풀면 다른 distribution에 대한 한 distribition의 expected log probability - entropy가 얼마나 작은지에 관한 값으로도 볼 수 있다. 일종의 거리라고 생각할 수 있고(그러나 distance metric은 아니라고 알고 있다) 따라서 0 이상의 값을 가진다.
여기서 entropy term이 없다면 q와 p의 분포가 비슷하지 않아도 비슷하게 하기 힘들어 질 것이다. 위에서 했던 first part만 maximize한 분포가 나와도 문제없는 상황이 나오는데, 좋은 상황이 아니다. 사실 위 그림을 직관적으로 봤을 때도 q와 p가 비슷하려면 p가 널리 퍼질 필요가 있다.

다시 이전으로 돌아가서 lower bound term을 보면, KL-Divergence로 나타낼 수 있다. 위의 전개를 거쳐 식을 정리하고 나면 기존 log probabilty를 KL-Divergence와 lower bound term의 합으로 나타낸 걸 볼 수 있고, KL-Divergence는 항상 양수이므로 앞서 봤던 lower bound가 성립하게 되는 것이다.
위 부등식이 등식이 될 수록 좋고, 이 말은 q와 p의 차이가 줄어들수록 KL-divergence 값은 작아질 것이고 부등식은 등식에 가까워진다. 따라서 KL divergence가 작아지도록 L_i가 log p(x_i)를 잘 approximate한 것이 된다.

그러므로 negative evidence lower bound, -L_i(p, q_i)를 최대화하는 것은 p(x_i)를 크게 할 것이고,
p와 q_i의 KL-divergence 값이 작아질수록 lower bound가 우리의 objective에 가까워져 더욱 효과적인 최대화가 가능하다.
KL-divergence 값이 크다면 lower bound를 maximize할 수는 있지만 objective가 될 수 없고, 작다면 objective가 되지만 lower bound를 maximize하려면 p(x_i)를 끌어올려야 한다. 그래서 q_i를 쓸 때 KL-divergence를 최소화하도록 선택해서 objective가 되도록 해야 하는 것 같다.
실제 훈련 시에는 L_i를 p, q_i 둘 모두에 대해 최대화한다.

실제 과정은 다음과 같다.
- L_i(p, q_i)의 theta에 대한 gradient를 계산한다. 즉 evidence lower bound의 gradient를 계산하는 것이다.
z를 q_i(z)로부터 sampling한 뒤 log p(x_i | z)에 근사하는 방식으로 구하는 듯 하다. - theta를 update하고, q_i가 lower bound를 maximize하도록 update한다.
- q_i에서는 mean, variance를 업데이트해야하는데 lower bound에서의 gradient를 사용해 gradient ascent를 사용.

이때 mean과 variance가 각 q_i마다 따로 존재하기 때문에 parameter 수가 데이터의 수에 비례하게 되고, 데이터 양이 커지면 문제가 될 수 있다.
이것을 해결하기 위한 아이디어는, 원래 q_i(z)를 p(z | x_i)에 approximate하는 게 목표였으니(coditional 구하기 어려워서 새 distribution을 만들어 estimate하는 것이라고 위에 적어놓음), 모든 mean과 variance를 학습하는 대신 각 data마다 mean, variance를 예측해주는 또다른 network를 만들자는 것이다.
현재 p_theta (generative model 자체), q_phi (주어진 data(img)에 대해 distribution을 예측. 정확히는 mean, variance pver z를 예측해주는 것) 2개의 model이 있다.

기존에 사용한 q_i를 q_phi로 대체해서 evidence lower bound를 q_phi에 대해 만든 amortized variational inference이다. 이때 phi는 lower bound 식에서 2번 나타나는데, 하나는 expectation의 distribution, 다른 하나는 entropy에서 나온다. 이에 대해 알아보자.

Entropy term은 conditional q_phi가 gaussian임을 이용해 쉽게 계산할 수 있으나, 그 앞의 항은 어렵다. 이때 expectation 내부 식이 phi에는 independent함을 이용해 내부 식을 새로운 함수 r(x_i, z)로 정의 후 새로운 함수 J(phi)를 만든다. 마치 reinforcement learning의 objective function과 비슷해서 그에 대한 policy gradient를 그대로 사용하면 된다고 한다. 그러나 policy gradient처럼 variance가 큰 문제가 있어 최선의 선택은 아니라고 한다. 더 나은 방법은 없을끼??

z를 mean, variance에 대해 나타내는 것으로 reparametrization trick을 사용하는 방법도 있다. 또한 epsilon은 phi에 independent하다. 여기서 objective를 epsilon에 대한 expected value로 reparametrization할 수 있다. 따라서 expectation을 phi에 independent하게 만들 수 있다. 이를 사용해 J의 gradient를 estimate할 수 있다.
- N(0, 1)로부터 M개의 epsilon들을 sampling한다. M=1도 꽤 좋다고 한다.
- 그리고 gradient를 epsilon들을 이용해 근사한다.
(Autodiff software의 힘을 빌리자)
Reinforcement learning에선 reward에 대한 derivative를 몰라서 이것이 불가능하나 여기선 가능하다고 한다.

Entropy가 아닌 KL-Divergence에 대해 나타내는 방법도 있다. 이 경우 expectation 안에 theta, phi 모두 들어가 있어, 둘 모두에게 depend해진다.
첫 네트워크에서 mean과 variance를 구하고 epsilon을 sampling해서 z를 구한 뒤, p(x_i, z)를 구한다. 이를 autodiff package로 backpropagation을 거쳐 theta, phi에 대해 gradient ascent를 진행하면 된다.
마치 phi로 encode, theta로 decode하는 것 같아 variational autoencoder라고 불린다고 한다. 다만 noise(epsilon)을 z에 넣는 것이 차이점이다. (Autoencoder는 시작 시 noise 추가)

정리하면,
Policy gradient는 discrete, continuous latent variable 모두 처리할 수 있으나 variance가 높고 multiple sample과 small learning rate가 필요하다는 단점이 있다.
Reparameterization trick의 경우 variance가 낮고 개발이 쉬우나, continuous latent variable에 대해서만 사용 가능하다.
이제 VAE를 다루기 위해 필요한 것들을 모두 알아보았다.
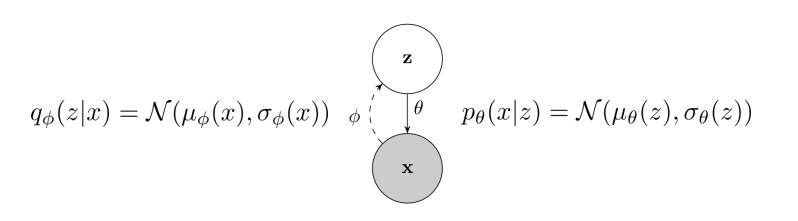
왼쪽의 q가 encoder part이다. x를 input으로 받아 z의 mean, variance를 출력한다.
오른쪽의 p가 decoder part이다. 앞서 구한 z의 mean과 variance를 바탕으로 sampling한 z를 input으로 넣어, 원래 구하고자 하는 x의 분포 - x의 mean과 variance - 를 출력한다. 이때 mean과 variance는 이미지의 모든 pixel에 대해 독립적으로 나온다.

펼처보면 위와 같다. 마지막에는 x에 대한 resulting distribution, p(x | z)를 획득한다.
L_i를 모든 이미지에 대해 구해서 평균낸 항을 최대화하도록 parameter들을 구한다.
이때 첫 번째 log term은 autoencoder의 objective와 유사하다. x_i를 mean, variance로 encode해서 z를 얻는 것으로 생각할 수 있다고 한다.
두 번째의 KL-divergence term은 분포 q_phi가 prior p(z)로부터 얼마나 떨어져 있는지에 관해 일종의 penalty를 주는 것으로 해석할 수 있다. 이 term으로 인해 encoded z가 p(z) (prior) 에서 sample한 것과 유사하도록, 즉 q_phi와 p라는 두 distribution이 서로 유사해지는 방향으로 학습하고, 따라서 decoder는 p(z)에서 sampling한 것을 바탕으로 realistic image를 생성한다.

요약하면 test 시 p(z)에서 z를 sampling, 그걸 기반으로 p(x | z)에서 x를 sampling한다.
(KL-divergence term이 encoded z를 p(z)와 비슷하게 만들어 주므로 그냥 p(z)에서 sampling하는 것이 가능!)

x에 기반한 y를 generate하는 conditional model도 가능하다. 식이 더 복잡해진 느낌이 드는데,

lower bound 식과 정확히 같은 형태이다.
(Conditional probability 역시 probability이다. x에 conditioned 되었으니, 위의 식에서 잠시 x를 가려 보자. 그러면 밑 식의 x가 y로 바뀌었을 뿐이지 정확히 같은 식이 된다.)
원리 역시 같다. p(y | x)는 복잡하지만 p(y | x, z)는 더 쉬울 것이니 이를 이용한다. Decoder는 p_theta(y | x, z)를 구할 것이고 encoder는 q_phi(z | x, y)를 구한다. Input에 x가 추가됨에 유의한다.
Test 시에는 p(z | x), p(y | x, z)에서 z, y를 차례로 sampling한다. 이때 p(z | x)는 gaussian처럼 fixed distribution일 수도, 학습된 distribution일 수도 있다.

Convolution을 사용한 VAE도 있다. 앞의 q_phi, 즉 encoder는 convolution, decoder는 transpose convolution이 된다. 이때 encoder 마지막에 FC layer로 각각 mean, variance를 뽑고 epsilon을 sampling한다. 이것들을 토대로 z를 생성 후 dimension을 조정해주고 transpose convolution 등의 upsampling으로 이미지를 만든다. Output은 역시 각 pixel에 대한 mean과 variance이다. 이후 negative log probability of the image와 KL divergence between p(z) and q_phi(z | x)를 사용해 loss를 구하고 backpropagation을 거친다(앞서와 같이?).
Representation을 따로 사용하고 싶을 경우 z를 사용한다. z 생성까지가 bottleneck representation이 된다.
Fully convolutional VAE를 만들 수도 있다. mean, variance에 대해 convolutional response map을 사용하고 나머지는 그대로 놓으면 된다. 다만 p(z), prior는 N(0, I)를 따르므로 각 dimension에 independent하나 convolution을 거치며 이미지의 각 pixel은 dependent할 가능성이 높고, 이에 KL-divergence term을 최소화하기 힘든 문제가 있다고 한다.

VAEs, 특히 conditional VAEs는 latent code z를 무시하기 쉽고 poor sample을 만들기 쉽다고 한다. 왜냐하면 conditional VAES는 처음에 z를 일종의 noise처럼 간주해 z를 어떻게 써먹어야 하는지 알아차리기 힘들고, objective의 한 부분이 z를 더욱 prior distribution처럼 보이게 하는 부분이라면 더욱 그렇다고 한다. (z를 uninformative하게 만들어서 쓸모없게 할 수 있다는 말이다)그래서 2가지 문제가 있는데, 1. latent code가 무시당함, 2. latent code가 잘 압축되지 않음 이다.1번의 경우 p_theta(x | z)가 사실상 p(x)처럼 여겨지는 문제로, 이렇게 할 시 reconstructing을 하면 input과는 영 관계가 없어 보이는 dataset의 average 같은 blurry한 이미지가 나온다고 한다.2번은 1번과는 반대의 문제로, z가 제대로 압축되지 못하고 너무 많은 정보가 담기는 나머지 q_phi(z | x)가 p(z)와 너무 다른 문제, 어찌 보면 encoder가 identity function인 문제라고도 할 수 있다고 한다(q가 제대로 학습된 것이 아니므로). 이때는 reconstructing은 잘 돌아가지만, z를 p(z)로 sampling하는데 q와 p가 너무 다르므로 output image는 unrealistic한 garbage가 나온다고 한다.
이는 KL divergence term으로 깔끔하게 정리할 수 있다. KL divergence가 너무 작은 경우가 1번, 너무 큰 경우가 2번 문제이다.

먼저 1번 문제의 경우, q_phi(z | x)가 x를 무시해 encoder의 output이 zero mean / unit variance가 되고, z에 x에 관한 정보가 없어 decoder는 z를 쓰지 않게 (p(x | z) --> p(x)) 된다. 이는 KL divergence가 너무 작은 것이니, 앞의 beta 값을 줄여서 KL divergence가 덜 중요하게 해서 VAEs가 KL divergence를 증가시켜도 딱히 penalty가 없게 한다.2번 문제는 x를 완벽히 reconstruct하긴 하지만 prior p(z)가 q_phi와 너무 차이나서 z를 prior에서 sample 시 decoder가 혼란스러워하며 쓰레기를 내뱉는다. 여기선 KL divergence가 큰 경우이니 (두 distribution의 거리는 KL divergence로도 표현할 수 있다), beta를 키워서 강제로 중요성을 키워 최대한 작아지게 해서 q_phi와 p가 비슷해지게 한다.
강의의 마지막 part에선 variational autoencoder와 유사하나 더 간단한 structure를 가지고 있고 훈련이 쉬운, invertible model에 대해 배운다.

이전엔 decoder에서 x의 mean과 variance, 즉 분포를 output으로 냈지만 이제는 deterministic function x = f(z)를 사용해 single output x를 낸다.
이때 variable을 바꾸는 formula를 보면 jacobian의 deterninat의 inverse를 원래 함수에 곱한 것을 볼 수 있다. z의 distribtion이 있고 ( = p(z) ) z는 x에 의해 deterministic하게 변환된 것일 때 ( z = f^(-1) (x) ), x의 density는 z의 density를 volume이 변한 만큼 modify하면 되는 것이다. (determinant의 경우, 기하학적으로 부피가 얼마나 변했는지에 관한 값으로도 볼 수 있는 것으로 암)
이때 z -> x로 가는 invertible한 mapping을 배운다면 det 계산이 쉬워짐을 이용하는 것이다. 더 이상 lower bound는 없고 정확한 probability / likelihood를 얻을 수 있다.

이러한 모델을 normalizing flow model이라고 한다. z는 여던히 N(0, I)와 같은 simple distribution이다. 이전과 같이 log probability를 maximize하는 것이 objective고, p(x)를 z에 대해 나타낸 식을 사용하면 위 식과 같이 나온다. 그러나 식에는 inverse function과 determinant가 있어 이를 쉽게 계산할 수 있는 특별한 architecture가 필요하다.
이 normalizing flow model은 inverse transformation의 여러 layer로 구성되어 있고, 이것을 만들기 위해 invertible layer를 만들 줄 알아야 하고, multiple invertible layer로 deep neural network를 만드는 법을 알아야 한다.

Layer들의 composition은 쉽다. 각 function들이 모두 deterministic하고, invertible의 composition은 역시 invertible하기 때문에 그냥 합쳐버리면 된다. 이 경우 log determinant는 각각의 log determinant를 더한 것이 된다.
그렇다면 이제 남은 건 invertible한 layer를 만드는 것이다.

일반적으로 사용하는 linear + ReLU layer는 ReLU의 존재로 인해 확실히 not invertible이다. 그래서 연산을 조금 뒤틀어, nonlinear 연산이 일어난 경우에도 layer가 현재 정보를 기억하게 하는 방법을 사용하면 될 것이다.
그래서 위 diagram과 같이 z를 두 부분으로 나눈다. 첫 번째 부분에 해당하는 output은 identity로 보내준다. 그리고, 두 번째 부분에 해당하는 output은, (z의 두 번째 부분) + (z의 첫 번째 부분을 nonlinearity 처리한 것)으로 만들어 준다.
이것이 invertible하다는 건 쉽게 생각할 수 있다.
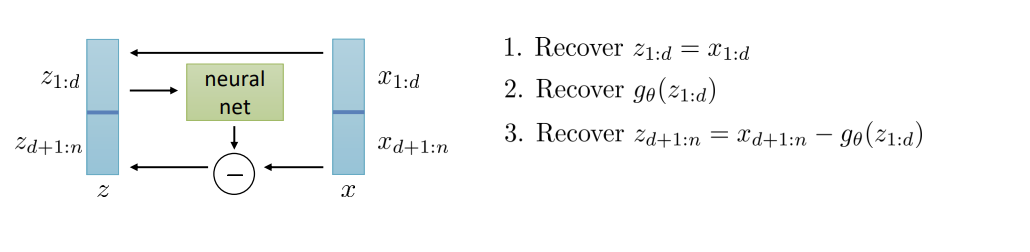
z의 첫 번째 부분은 x를 그대로 가져가면 되돌릴 수 있고, 두 번째 부분은 x의 두 번째 부분에서 z의 첫 번째 부분을 nonlinearity 처리한 것을 빼 주면 된다.

Jacobian 역시 살펴봐야 한다. 두 부분으로 z, x를 나누었으니 jacobian은 block matrix처럼 취급할 수 있다. 그런데 이를 구해보면 위와 같이 lower triangular matrix가 나오고 이 matrix의 determinant는 diagonal term을 모조리 곱한 것, 즉 1이 된다.
따라서 간편하지만 scale을 바꾸지 못해 representation이 종종 제한받는 경우가 생겨 정말 복잡한 distribution을 학습하기는 어렵다고 한다.


간단한 MNIST나 사람 얼굴의 경우 괜찮은 generation을 보이지만, 컬러 숫자, CIFAR-10 등 데이터가 복잡해지자 뭔가 이상해짐을 볼 수 있다.

그래서 조금 더 expressive한 방법이 나왔다. 이제 neural network는 2개가 된다. x의 첫 부분은 같으나 두 번재 부분의 경우 scaling network h를 거친 z의 첫 부분, bias network g를 거친 x의 첫 부분을 z의 두 번째 부분에 곱해주고 더해줘서 만든다. Nonlinearity로 exp를 사용하는 이유는 곱해지는 것을 0이 아닌 양수로 만들기 위함이다. ReLU는 0이 생겨 그 position에 해당하는 부분은 elementwise product로 인해 정보가 아예 사라져버리기 때문이다. 이제 jacobian은 1이 아니기에 volume을 보존하지 못하고, 따라서 더 expressive한 것이 나온다.


Normalizing flow model은
- Lower bound만 계산하는 VAE와 다르게 정확한 probability / likelihood를 계산 가능하고
- 따라서 더 이상 lower bound가 필요하지 않으며
- 개념적으로도 더 간단하다
하지만,
- 따로 특별한 architecture가 필요하고,
- z는 x와 반드시 같은 dimensionality를 가져야 한다는 단점이 존재한다. 이는 high-resolution image에서 큰 문제로 작용하는데, VAE의 경우 z의 dimensionality가 x에 비해 훨씬 작을 수 있으나 이것은 그렇지 않아 계산이 매우 많아질 수 있다.