[CS182] Lecture 10 - Recurrent Networks

CS 182: Deep Learning

 

 

이번 강의에선 recurrent network를 배운다.

 

지금까지 봤던 CNN은 input의 크기가 고정되어 있었다.

그런데 만약, 문장(단어의 수가 문장마다 다름)이나 소리, 동영상(길이가 각각 다름)인 경우 크기가 계속해서 달라진다.

 

간단히 떠올릴 수 있는 아이디어는, 가장 긴 sequence에 맞춰 zero padding을 붙여주는 것이다.

그러나 sequence의 길이가 길어진다면 별로 좋은 생각이 아니게 된다. 이를테면 최대 문장 길이가 1000개의 단어일 경우, 10개의 단어로 이루어진 문장에 990개의 0을 붙이는 건 딱 봐도 별로이지 않은가?

 

 

다른 방법은, sequence의 각 element 당 layer를 두는 것이다.

자연스럽게 layer의 수는 input의 수가 된다.

각 layer당, 새로 들어오는 x와 이전 layer의 output을 input으로 받아 처리한다.

다만, 성능은 좋지 않다. 이유는 후술하겠다.

 

다시 주제로 돌아와서, input sequence의 크기는 각기 다르니 상대적으로 짧은 sequence의 경우 missing layer가 생긴다.

이 경우, input 앞의 layer에서의 activation은 0으로 설정해준다. 따라서 첫 layer에선 input과 zero vector를 concatenate해서 input으로 사용한다.

 

Sequence가 짧을수록 거치는 layer 수가 줄어들어 확실히 zero-padding보다 효율적이다.

그런데 sequence가 길어질수록 weight matrix가 많아지고, 초반 부분의 weight는 길이가 긴 sequence만 거칠 수 있어 제대로 학습을 하지 못할 것이다.

 

 

그래서 나온 생각이 weight sharing이다. 이제 W는 모든 layer에 대해 똑같이 사용되고, bias도 마찬가지이다.

Layer를 원하는 만큼 만들어도 상관이 없고, 위에서 언급한 단점들이 사라진다.

이러한 구조의 model을 recurrent neural network라고 하고,

variable-depth network라고도 한다고 한다.

 

자신의 activation을 그대로 input으로 활용하고 weight를 공유함을 의미하는 그림이다. 이는 일반적인 neural network를 time dimension으로 확장시킨 것으로도 생각할 수 있겠다.

 

 

그렇다면 RNN을 학습시키는 방법을 한번 알아보자.

CNN을 학습할 때 backpropagation을 사용했던 것처럼 이번에도 backpropagation을 사용한다.

 

잠깐, 그런데 여기선 모든 weight를 공유하지 않는가? 이전처럼 backpropagation을 진행하며 k번째 layer에서 weight에 대한 gradient를 구하면, k+1번째에서 구한 gradient를 그대로 덮어써버릴 것이다. (매 layer마다 dL/dW가 계속해서 덮어씌워짐)

 

 

그래서 delta를 완전히 바꾸는 것이 아닌, 기존 gradient에 계속 더해주는 변형된 backpropagation을 사용한다.

알고 보면 당연?한 것인데, 새 activation의 input이 x와 이전 step인 h(x)라고 해 보자. g는 현재 step, f는 전체 RNN이다.미분하고 나면 chain rule에 의해 더해지는 형태가 된다. 따라서 모든 step에 대해 생기는 gradient를 더해주는 것이최종 gradient가 됨을 알 수 있다.

 

 

Input의 size가 다양한 경우도 있었으니, output의 size도 다양할 수 있다.예시로는 image에서 text caption 작성, video sequence 생성 등이 있다.

 

이제 각기 다른 layer마다 output이 존재하게 된다. 모든 output은 각각의 loss를 가지고, 전체 loss는 저걸 전부 합친 것이다.Output을 산출하는 function을 decoder라고 하는데, softmax가 같이 있는 linear layer일 수도 있고, 사실 뭐든 될 수 있다.

 

이 역시 backpropagation을 진행해서 학습시킨다.

 

 

그런데 이 computational graph만 보기엔, 과정이 조금 불분명해 보인다.

Recurrent의 특성을 살린 다른 그래프를 한번 살펴보자.

 

y_f는 각 layer의 output이 되면서, 동시에 다음 layer의 input으로 사용된다.

이렇게 multiple output이 있을 경우, 전체 delta는 output에서의 delta를 모두 더한 값으로 계산하면 된다.

이것이 backpropagation algorithm의 generalization이다.

 

 

Multiple input & output인 경우, 일반적으로는 위와 같이 된다.

 

---

 

 

최대 1000개의 단어를 가진 문장이 있다고 생각해보자. 이 문장이 RNN의 input으로 사용된다면,

RNN엔 1000개의 layer가 있는 것과 마찬가지다. 즉, RNN은 일반적으로 굉장히 깊은 network이다.

이렇게 깊은 network에서 backpropagation algorithm을 거치면, 자연스럽게 gradient vanishing / exploding gradient 문제가 발생할 가능성이 높아진다. (이를 해결하려면 jacobian들의 eigenvalue들이 1에 가까워야 한다)

 

사실 exploding gradient는 그렇게 큰 문제는 아니다. 앞선 강의에서 나왔던 "gradient clipping"을 통해 어느 정도 완화가 가능하기 때문이다. 진짜 문제는 vanishing gradient이다. 이는 사실 정말 심각한 문제이다. 직관적으로 생각했을 때, earlier step으로 갈수록 이전 step들의 gradient가 도달하지 못해, network가 정보를 잘 기억할 수 없게 되기 때문이다.

 

역시 기본적인 아이디어는 jacobian(의 eigenvalue)가 1에 가깝게 하는 것이다.

다만, 쓸데없는 정보까지 기억할 이유가 없으니 network가 기억하길 원할 때만 기억하는 것이 중요하다.

 

직관적으로 생각해보자.

이전 step을 기억하고 싶다면, 이전 step의 gradient를 1에 가깝게 하고 싶을 것이고,

그렇지 않다면 gradient를 0에 가깝게 해서 정보를 조절할 수 있을 것이다.

이를 위해 forget gate를 추가한다. 

기억할 것이라면 f_t의 값을 1에 가깝게 해 이전 cell state의 정보를 유지할 것이고

아니면 0에 가깝게 해, 새로운 memory인 g_t로 대체하는 원리이다.

 

 

여기서 LSTM(Long short-term memory) cell이 등장한다. 복잡해 보이지만, 천천히 살펴보자.

• 각 cell에서는 cell state와 hidden state를 계산해 다음 layer에 전달한다.
  우선 말해두자면 cell state는 long-term memory,
  hidden state는 short-term memory의 역할을 한다.
• Input과 이전의 hidden state를 받아 concatenate한 후 linear layer를 거친다.
  결과물로 hidden state와 같은 dimension의 4개의 vector가 쌓인 형태가 나온다.
  (이를 편의상 Z로 지칭하겠다)
  (이 4개의 벡터는 previous step에 의해 결정되는 것이다.)
• 먼저 f_t는 Z에 쌓인 4개의 벡터들 중 가장 위의 벡터를 nonlinearity에 통과시킨 것으로,
  이는 "forget gate"이다. (앞서 봤었다) "앞의 정보를 기억할지 말지에 대한 정도"를 나타낸다.
• 다음은 i_t로, Z에 쌓인 4개의 벡터들 중 두 번째 벡터를 nonlinearity에 통과시킨 것으로,
  "input gate"라고 한다. "Cell에서 얼마나 modification을 하고 싶은지에 대한 정도"를 나타낸다.
• 세 번째는 g_t로, 4개의 벡터들 중 세 번째 벡터를 nonlinearity(여기선 tanh이나, relu 등을 써도 된다)
  에 통과시킨 것이다. "현재 Cell에서의 modification 자체"를 나타낸다.
• i_t와 g_t를 pointwise product로 계산해서 새로운 modification memory가 cell에 들어간다.
• 네 번째는 o_t로, "output gate"이다. 가장 마지막 벡터를 nonlinearity에 통과시켜 얻는다.
  새 cell state에 곱해져서 다음 hidden state를 설정하는 데, 그리고 해당 layer에서 output을 생성할 때 사용한다.

a_t에는 nonlinearity가 가해지지 않음을 볼 수 있다. 이로써 derivative 형태가 좋아지고,다른 hidden state 구역에서의 non-linearity modification / readout으로 nonlinearity의 이점도 챙긴다.Output gate, input gate를 쓰지 않아도 잘 돌아갈 때가 있다고 한다. 이 모델은 다양한 방법으로 단순화가 가능하다.

 

LSTM의 cell state는 매 step마다 간단히 변형되고, hidden state는 linear operation에 의해 매 step마다 크게 변한다.

따라서 위에서 언급했듯이 cell state는 long-term memory, hidden state는 short-term memory이고

이 두 가지를 모두 사용하기에 LSTM은 좋은 성능을 낸다고 한다.

 

일반적으로 RNN은 거의 항상 input과 output을 모두 가진다.

Naive RNN은 못 쓸 정도이나, LSTM은 좋은 성능을 가진다. 다만 hyperparameter tuning이 조금 어렵다.

이외에 transformer 등의 다른 대안도 있고, LSTM을 조금 단순화한 GRU 등의 변형 버전 역시 선택지에 있다.

 

---

 

대부분의 경우는 하나의 input과 output을 가지는데, 여러 input, output을 사용할 떄가 많다.

보통 이런 경우는 output 간의 연관성이 있기 때문인데 (structured prediction)

문장을 생성하는 경우를 가정해보자. 단어 사이 연관성 정보가 없다면 이상한 문장, 유효하지 않은 문장이 결과로 나올 수 있다.

따라서, input(word) 간의 연관성을 나타내주는 covariance가 중요해진다.

 

이는 과거 output이 미래 output에 영향을 주도록 해서 해결한다.

Output이 structured sequence인 모든 RNN에서 이 아이디어가 사용된다고 한다.

(때문에 one input - multi output 구조를 찾아보기 힘들다고 한다)

 

이러한 모델을 훈련 시, input은 entire training sequence가 되고, 이때 ground truth를 하나씩 옆으로 옮겨주어야 한다.

 

여기엔 짚고 넘어가야 할 것이 있다.

굉장히 긴 sequence의 complex model을 훈련 시, 예기치 못한 문제가 발생할 수 있다는 점이다.

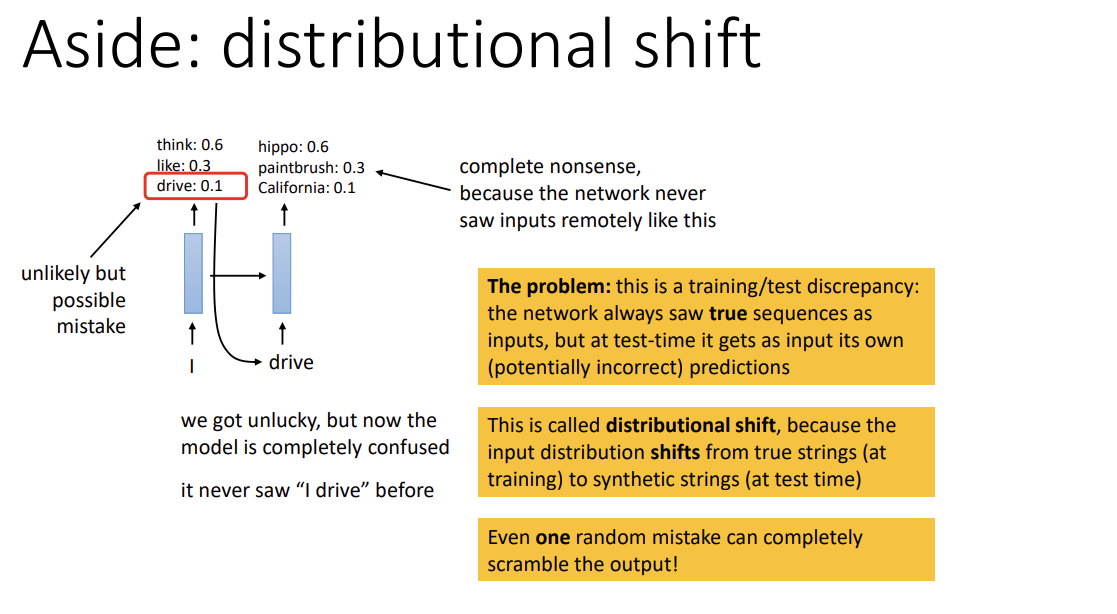
만약 network가 실수로 잘못된 sample을 골랐을 때, ground truth와 너무 달라져 network의 output이 이상해질 수 있다.

Train 중에는 true sequence만 보지만 test 중 잘못된 prediction을 해 다시 input으로 올 수가 있고,

이 실수가 계속해서 쌓이다 보면 결국 의미 없는 결과가 나온다.

이 현상을 distributional shift라고 한다. Input distribution이 true string으로부터 shift했기 때문이다.

 

Scheduled sampling이라는 방법을 사용해 해결할 수 있다. 매 step마다의 input을 랜덤한 확률에 따라

true input과 이전 step의 output 중 골라서 주는 것이다. 이제 network는 test time에 덜 혼란스러워한다.

이 확률 p는, 시작 부분에선 아직 model prediction이 제대로 된 상태가 아니니 대부분 ground truth를 주고,

끝으로 갈수록 distribution shift를 완화하기 위해 model의 prediction을 준다.

이는 깊은 모델, 복잡한 모델에서 도움이 된다.

 

이미 몇 가지를 봤지만, RNN을 사용하는 방법에는 input과 output의 개수 등을 고려해 여러 가지 방법으로 사용 가능하다.Many-to-many에는 모든 input을 읽고 output으로 변환하거나, 즉시 변환하는 2가지 방법이 있다.

 

RNN을 다른 모델 위에 쌓을 수도 있다. 위의 예시는 input이 CNN encoder, output이 RNN decoder이다.

 

당연히 RNN 위에 RNN을 쌓을 수도 있다. 이런 여러 layer의 RNN은 꽤 흔하게 사용된다.

LSTM으로도 가능하고, 특히 이 경우는 convolutional layer를 대체 가능하다고 한다.

 

Speech recognition같이, 전체 문장을 보기 전에 섣불리 추측하기 힘든 경우도 존재한다. 이런 상황은,

forward와 backward 방향으로 모두 학습하는 bidirection model로 해결할 수 있다.

(Forward RNN 위에 backward RNN을 쌓아, backward 시 과거와 미래 정보를 모두 가지게 됨)