2022. 8. 7. 02:27ㆍML, DL/CS182
CS 182: Deep Learning
Head uGSI Brandon Trabucco btrabucco@berkeley.edu Office Hours: Th 10:00am-12:00pm Discussion(s): Fr 1:00pm-2:00pm
cs182sp21.github.io

4강에선 optimization에 대해 배운다.
앞서 2강에서 짧게 짚고 넘어갔던 gradient descent는 , loss landscape 상에서 현재 gradient의 반대로 움직이며 optimal한 지점을 찾아나간다.
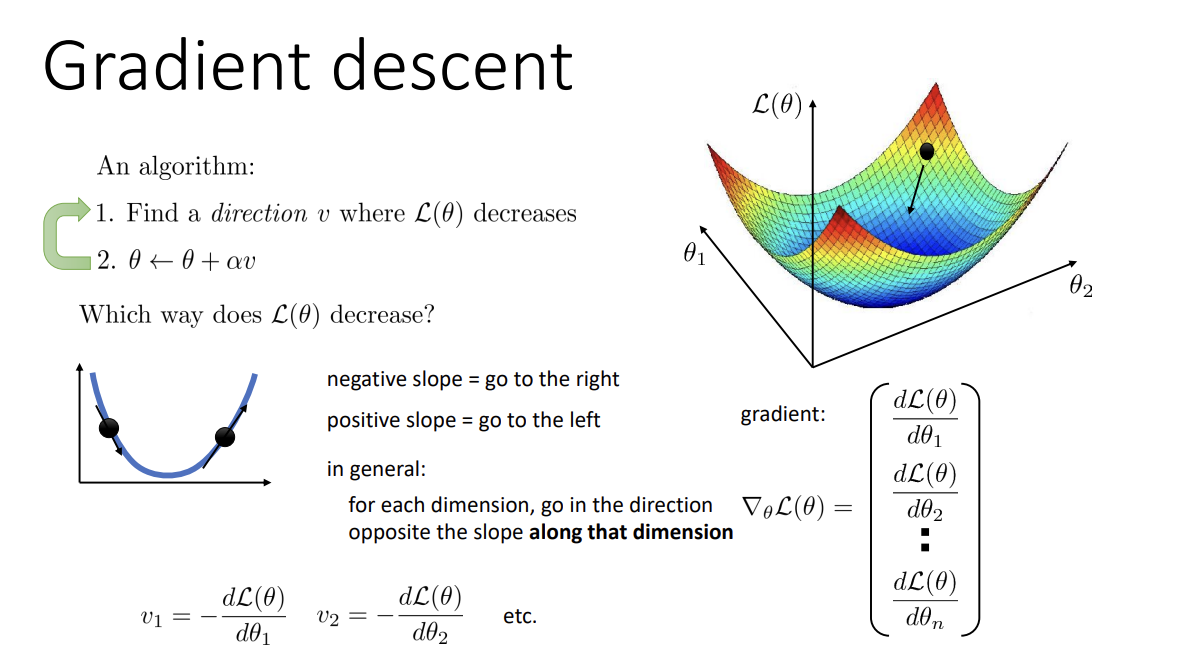
그러나, 항상 optimum에 도달한다는 보장은 없다. Steepest direction이 꼭 optimal하지 않을 수 있다는 뜻이다.

NLL(Negative Log-Likelihood) loss의 경우(regression에서 사용) 대체로 loss landscape가 convex 형태임이 보장되어 있으나, trivial하지는 않다.
Nice한 형태의 convex는 optimum에 도달하는 것이 거의 확정적이나, 그렇다고 모든 convex 형태에서 gradient descent가 잘 작동하지는 않는다고 한다.

이 이미지의 그래프들에서 볼 수 있듯, optimum이 하나여도 non-convex일 수 있다.
사실 위의 loss surface는 굉장히 이상적인 형태이다. 즉, 실제 상황에서 저런 그래프를 볼 확률은 극히 희박하다는 것이다.
데이터가 다차원일 경우가 대다수이기에 visualize하기도 쉽지 않다.

이를 시도한 논문도 있다고 한다. 위의 괴상한? 협곡 같은 그림에 plateau, local optima라는 용어가 있는데,
loss landscape에서 우리가 조심해야 할 형태 중 하나이다.
Loss landscape를 기하학적인 면에서 보면,

이와 같은 3가지의 형태를 조심해야 한다. 하나씩 살펴보자.
1. Local optima

전체 loss에 대한 optimum이 아닌, 일부 지역에서의 optimum인 지점을 이른다. Gradient descent 과정 중 이곳에 converge할 수 있어 neural network에 대한 걱정거리 중 하나이다.
그러나 재미있게도, parameter가 많아질수록 local optima는 큰 문제가 되지 않는다고 한다. 정확히는 local optima와 global optima의 차이가 크지 않아, 괜찮은 local optima를 찾는 것이 목표가 되기도 한다고 한다.
2. Plateaus

Neural net의 loss landscape에서 흔히 등장한다. 한국어로는 "고원"이라는 뜻을 가지고 있고, 이름처럼 평평한 구간, 즉 gradient가 정말 작은 부분을 뜻한다. 만약 learning rate가 작게 설정되어있다면 plateaus를 벗어나지 못하고 갇혀버릴 수 있다.
3. Saddle points

미적분학 시간에 배웠지만 기억은 잘 나지 않을 saddle point는 high-dimension에서 흔히 나오는 현상이다.
간단히 설명하자면, 어떤 dimension에 대해선 local minimum이나 또 다른 dimension에 대해선 local maximum인 지점을 뜻한다. 즉, partial derivative는 0이나 dimension별로 주변의 함수의 값이 증가할 수도, 감소할 수도 있는 곳이다.
Saddle point에 근접할수록 gradient는 작아지고, 마치 plateaus의 경우처럼 step이 굉장히 작아지게 된다. 또한 neural network에서 대부분의 critical point가 saddle point이다.

참고로 critical point의 경우, second derivative인 hessian을 통해 max / min / saddle을 구분하는데,
Negative definite (diagonal entry들이 negative)인 경우가 maximum,
Positive definite (diagonal entry들이 positive)인 경우가 minimum,
Indefinite (diagonal에 positive, negative entry 모두 있는 경우) saddle point이다.
이런 무수한 함정들 속에서 대체 어느 방향으로, 어느 정도를 가야 할까?
우선, 방향에 대해 알아보자.

Newton's method를 통해 해석적으로 올바른 direction을 찾을 수 있다. 그러나 위 이미지에서 볼 수 있다시피 taylos series의 2차 근사를 이용했다.
반드시 optimal한 지점을 해석적으로 찾을 수 있다는 2차함수의 장점을 이용하기 위해 2차 근사를 사용하나,
계산에 hessian의 inverse가 필요하고, 그것을 계산하려면

우리의 컴퓨터로는 O(n^3)의 시간복잡도가 필요하다. 못 쓴다는 뜻이다.
그래서, second derivative를 사용하지 않는 무언가를 필요로 한다.

이 momentum이란 방법은, (직관적으로)다른 방향은 상쇄시키고 같은 방향은 증폭시켜 최적점을 향해 가는 방식이다.
벡터의 계산을 생각하면 쉽게 와닿는다.

실제 update rule은 다음과 같다. 이전엔 단지 gradient의 반대로 움직였다면, 이젠 과거의 방향을 기억해서 움직이는 방향에 섞어주는 것이다. 따라서 opposite direction은 상쇄되고, similar direction은 증폭될 것이다.
Newton's method의 장점을 낮은 비용으로 챙길 수 있다.
다음으로, 어느 정도를 가야 하는지에 대해 알아보자.

Gradient의 sign은 우리에게 direction을 알려주지, magnitude를 알려주지는 않는다.거기다 optimization을 거치며 gradient의 magnitude가 크게 변한다면, learning rate 조절이 더욱 어려워진다.그러니, gradient의 각 dimension마다 magnitude를 "normalize"하는 건 어떨까?

먼저 알아볼 알고리즘은 RMSProp이다.간단히 말하자면, 갱신되는 gradient의 양을 각 방향의 평균 길이로 나눈 느낌이다. 이때 과거의 s_k 정보를 활용한다.

다음은 AdaGrad이다. 앞의 RMSProp은 과거 정보와 현재 gradient의 magnitude를 일정 비율을 맞추며 더해줬다면, Adagrad는 현재 gradient의 magnitude를 계속 더해간다. 즉 update되는 gradient의 양이 점점 작아지는 것이다.
AdaGrad는 convex problem에 특히 효과적이다. Learning rate가 시간에 따라 감소하니, optimum에 보다 천천히 접근이 가능하다. 이와 비교해 RMSProp의 경우 learning rate가 효과적으로 줄어든다고 할 수는 없고, 따라서 oscillation이 발생할 수 있다. 그러나 non-convex problem의 경우, learning rate가 너무 빨리 줄어들기 때문에 별로 좋지 않다.

다음은 Adam이다. Momentum과 RMSProp을 결합시킨 듯한 알고리즘으로, 두 개의 moment estimate를 가진다.
m_k는 momentum의 g_k와, v_k는 RMSProp의 s_k와 비슷한 형태이다.
또한 실제로 parameter update에 사용하는 estimate는 m_k와 v_k를 살짝 변형한 형태인데,
저 값들은 (0에서 시작 시) 초기에 너무 작고 갈수록 커지는, 뭔가 이상한 상황이 되므로 이를 위해 초기에 m_k의 크기를 키우고, 시간이 지나면 수치가 조절되도록 한 것이다.
Naive한 gradient descent는 모든 데이터를 바탕으로 gradient를 계산하므로 (당연히) 느릴 수 밖에 없다.이를 개선하기 위해, dataset으로부터 무작위 minibatch를 샘플링해서, 이 batch를 이용해서 gradient를 구하는 것을Stochastic gradient descent라고 한다.

어느 정도의 noise가 있을 수는 있으나, 무작위 sampling이므로 unbiased이기 때문에 결국 같은 결과로 갈 것이다.
다만 실제 적용 시에는 random sampling 자체가 느린 이유로, 아예 처음에 dataset을 무작위로 섞어버리고
batch를 연속적으로 뽑아내는 방식을 사용한다고 한다.
Learning rate는 어떻게 설정할까?

낮은 learning rate는 optimization 과정을 오래 할 경우 괜찮으나, 시간이 오래 걸리고 deep learning에선 plateaus에 갇힐 수 있어 좋지 않다.
높은 learning rate는 초반 학습 속도가 굉장히 빠르나, oscillating 현상이 발생할 수 있어 최종 결과가 그리 좋지는 않을 것이다.
그러면 자연스레 이런 생각을 할 수 있다. '그냥 epoch에 따라 다른 learning rate를 쓰면 안 되려나?'
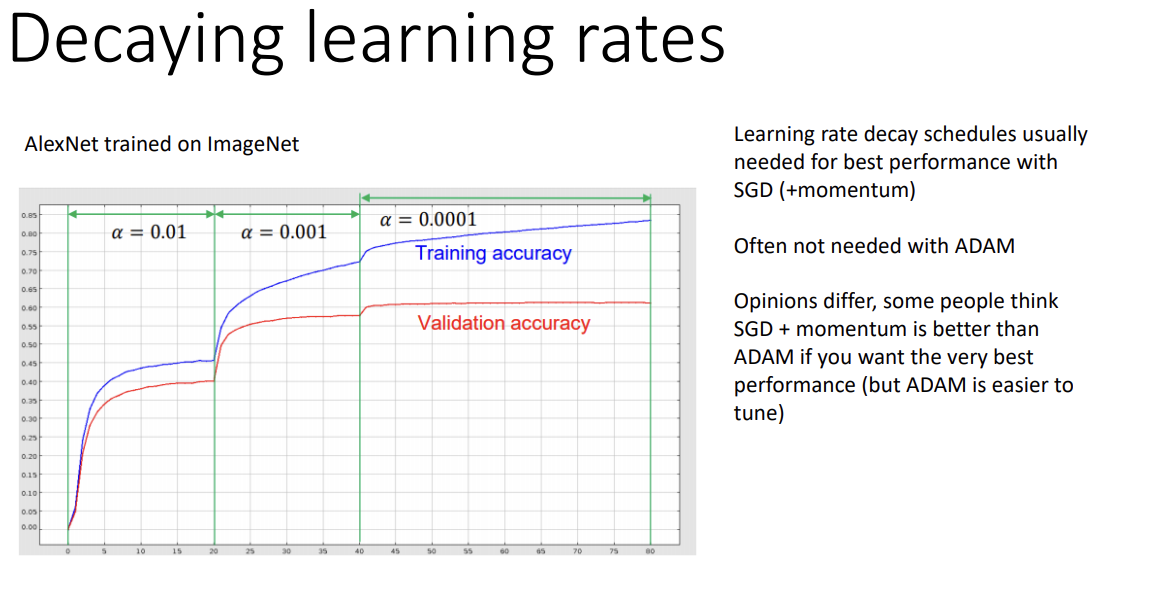
이것을 decaying learning rates라고 한다. 실제로 위의 AlexNet의 accuracy graph를 보면, epoch에 따라 learning rate의 값이 다른 것을, 그리고 값이 바뀔 때마다 accuracy가 상승함을 볼 수 있다.
이 방법은 주로 SGD와 SGD + momentum에서 사용하는 방법이고, Adam에서는 필요하지 않을 때도 있다고 한다.
"정말 좋은 성능"을 원한다면 decaying learning rate를 적용한 SGD+momentum이 Adam보다 낫다는 의견도 있는데, Adam의 parameter tuning은 상대적으로 쉬워서 일장일단이 있다.
마지막으로 gradient descent의 tuning에 대해 간단히 알아보겠다.

- Batch size는 클수록 gradient의 noise가 감소하고 보다 위험성이 줄어드나, 비용이 비싸진다.
- Learning rate는 가능한 한 가장 큰 값을 사용하고, 시간에 따라 감소하는 것이 좋다.
- Momentum은 0.99를 주로 사용한다.
- Adam parameter의 경우 default setting을 그대로 사용하는 편이다.
Hyperparameter는 optimization을 위한 parameter이기에 training loss를 통해 tuning한다.그러나 종종 validation loss를 사용하기도 한다고 한다.(Stochastic gradient 그 자체로도 regularizer의 기능이 있을 수 있다는 연구가 많은데, regularization에 관련된 것은 validation loss를 사용하기 때문.)
'ML, DL > CS182' 카테고리의 다른 글
| [CS182] Lecture 8 - Computer vision (0) | 2022.08.10 |
|---|---|
| [CS182] Lecture 7 - Getting Neural Nets to Train (0) | 2022.08.09 |
| [CS182] Lecture 3 - ML Basics 2 (0) | 2022.08.05 |
| [CS182] Lecture 2 - ML Basics 1. (0) | 2022.08.04 |
| [CS182] Lecture 1 - Introduction (0) | 2022.08.04 |